正文
我们考虑一个关于求和的问题
\(\forall i\),求\(∑_{j⊂i}a_j\),这里\(j\subset i\)
的定义可以很宽泛,我们可以将其定义为\(j|i\),也可以是j的二进制表示是i的二进制表示的子集等等
显然一种暴力的方法就是枚举i的所有子集,考虑优化的话,我们可以尝试前缀和,因为显然如果有\(j⊂z,z⊂i\),我们可以将j的贡献都先算在z上面再传给i,而不必一个个来
但是这样的话,就涉及到了高维的前缀和处理
先来看看一维前缀和是怎么写的
1
2
3
4
| for(int i=1;i<=n;++i)
{
a[i]+=a[i-1];
}
|
然后是二维前缀和,这里我们一般用容斥来处理
1
2
3
4
5
6
7
| for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
}
}
|
如果到了三维的话,也是可以容斥的,写起来就有点烦
实际上除了容斥,我们还有另外一种写前缀和的方法
二维
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
sum[i][j]+=sum[i][j-1];
}
}
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
sum[i][j]+=sum[i-1][j];
}
}
|
这个其实很好理解
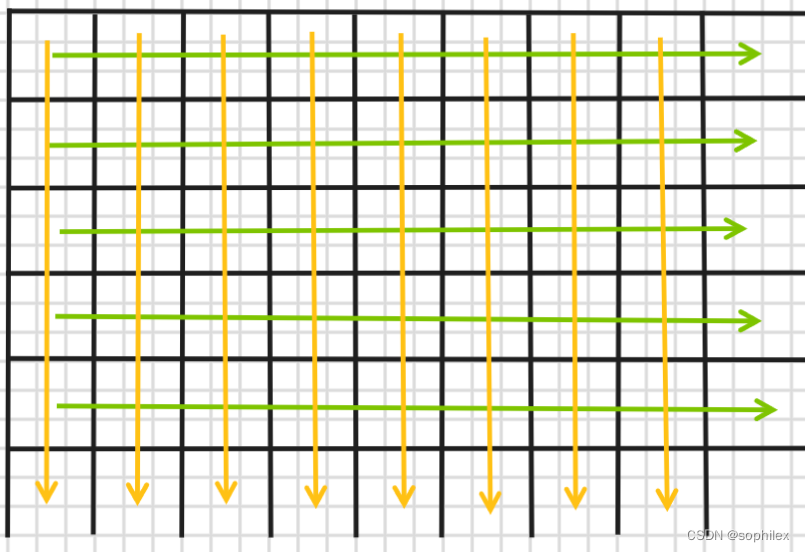
我们先按绿色方向把每一层的前缀和都给做出来,然后再沿黄色方向做一遍前缀和,按顺序从小往大走的话,显然我们会把第一维(行)的前缀和算进去。
所以不难得到三维的前缀和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
for(int k=1;k<=q;++k)
{
sum[i][j][k]+=sum[i-1][j][k];
}
}
}
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
for(int k=1;k<=q;++k)
{
sum[i][j][k]+=sum[i][j-1][k];
}
}
}
for(int i=1;i<=n;++i)
{
for(int j=1;j<=m;++j)
{
for(int k=1;k<=q;++k)
{
sum[i][j][k]+=sum[i][j][k-1];
}
}
}
|
那么如果扩展到了n维会怎么样?
思路跟上面是一样的,就是一维一维的做前缀和
二进制子集前缀和
考虑一开始的问题: \(\forall i,0\leq i\leq
2^n-1\),,求\(∑_{j⊂i}a_j\)
,其中 j属于i 定义为j的二进制表示是i的二进制表示的子集
1
2
3
4
5
6
7
8
9
10
| for(int j=0;j<n;++j)
{
for(int i=0;i<(1<<n);++i)
{
if(i&(1<<j))
{
dp[i]+=dp[i^(1<<j)]
}
}
}
|
因为是正序枚举的,所以\(i^(1<<j)\)是是当前这一维度,而此时i还在上一维,所以这样就实现了高维的前缀和。这样的时间复杂度是\(O(n2^n)\),而如果去枚举子集来做前缀和的话,时间复杂度是\(n^3\)的。
我们来看一些具体的应用
ARC 100 E - Or Plus Max
大意: 给定一个长度为\(2^n\)的数组,对于每一个\(k,1<=k<=2^n-1\),求出最大的\(ai+aj\),其中\(iOR j<=k\)
思路: 关键就是如何处理\(i or
j<=k\),不难发现这蕴含的意思其实就是\(iorj\)的结果是\(k\)的二进制表示下的子集
所以我们直接跑高维前缀和,维护一下每一个\(k\)对应的能够用的最大值以及次大值即可
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
ll n;
ll mas[N],sec[N],dp[N];
void upt(ll id,ll val)
{
if(val>=mas[id])
{
sec[id]=mas[id];
mas[id]=val;
}
else if(val>=sec[id])
{
sec[id]=val;
}
}
void solve()
{
cin>>n;
for(int i=0;i<(1<<n);++i) cin>>mas[i];
for(int j=0;j<n;++j)
{
for(int i=0;i<(1<<n);++i)
{
if(i&(1<<j))
{
upt(i,mas[i^(1<<j)]);
upt(i,sec[i^(1<<j)]);
}
}
}
for(int i=1;i<(1<<n);++i)
{
dp[i]=max(dp[i-1],mas[i]+sec[i]);
cout<<dp[i]<<endl;
}
}
int main()
{
solve();
return 0;
}
|
再看一道
给定一个数组,问里面有多少个数字满足\(a_i\:
and\: a_j=0\)
思路:
显然对于一个数\(a_i\),我们找到它的二进制表示的补集\(Q\),那么\(Q\)的所有子集出现过的次数就是\(a_i\)的贡献,所以我们还是可以通过高维前缀和来处理
代码不写了,题源也找不到,自己意会一下
那么上面都是二进制枚举子集的前缀和,如果是枚举超集的话,那其实叫后缀和会更加合理一些吧
二进制超集后缀和
代码也很好写,无非就是把原本为0的地方改成1
1
2
3
4
5
6
7
8
9
10
| for(int j=0;j<n;++j)
{
for(int i=0;i<(1<<n);++i)
{
if((i&(1<<j))==0)
{
dp[i]+=dp[i^(1<<j)]
}
}
}
|
Jzzhu and Numbers
大意:

\(n,a_i<=1e6\)
思路:
不考虑复杂度的话我们有一个非常套路的容斥做法。考虑性质Ai表示子集与之后第i位为1,那么我们的答案其实就是
\[
|\Omega -A_1\bigcup A_2...\bigcup A_{20}|=\\
\sum_{i=0}^{20}(-1)^i\sum_{1\leq j_1 < j_2...<j_i \leq 20
}|A_{j_1}\bigcup A_{j_2}...A_{j_i}|
\] 显然就可以状压枚举,这样的时间复杂度是\(O(n*1e6)\),考虑优化。
注意到对于\(|A_{j_1}\bigcup
A_{j_2}...A_{j_i}|\),我们记满足对应所有性质的元素的个数为\(k\),则该集合的大小就是\(2^k-1\),那么什么元素会满足这些性质呢?就是二进制为其超集的元素呗,其价值就是1.
所以我们只要做一遍超集后缀和即可,时间复杂度来到\(O(20*1e6)\)
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const ll N=1e5+10;
const ll mod=1e9+7;
ll n,cnt=0,a;
ll mas[N];
ll up=20;
ll vis[30];
ll dp[(1<<20)+10];
ll ksm(ll x,ll y)
{
ll ans=1;
while(y)
{
if(y&1) ans=ans*x%mod;
x=x*x%mod;
y>>=1;
}
return ans;
}
ll gt()
{
ll tot=0;
ll fl;
for(int i=1;i<=n;++i)
{
fl=1;
for(int j=0;j<up;++j)
{
if(!vis[j]) continue;
if((mas[i]&(1<<j))==0)
{
fl=0;
break;
}
}
if(fl) tot++;
}
return ((ksm(2,tot)-1)%mod+mod)%mod;
}
void solve()
{
cin>>n;
for(int i=1;i<=n;++i) cin>>a,dp[a]++;
for(int j=0;j<up;++j)
{
for(int i=0;i<(1<<up);++i)
{
if((i&(1<<j))==0) dp[i]+=dp[i^(1<<j)];
}
}
ll ans=0;
for(int s=0;s<(1<<up);++s)
{
cnt=0;
for(int i=0;i<up;++i) if(s&(1<<i)) cnt++;
if(cnt%2) ans=((ans-ksm(2,dp[s])+1)%mod+mod)%mod;
else ans=((ans+ksm(2,dp[s])-1)%mod+mod)%mod;
}
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}
|
然后我们看看一开始提出的第二种定义
\(\forall i,0\leq i\leq
2^n-1\),,求\(∑_{j⊂i}a_j\)
,其中$ ji$ 定义为\(j | i\)
显然\(j|i\)蕴含的意思是,对于每一个质因子p,j蕴含的p的幂次不大于i蕴含的p的幂次,所以这里还是一个子集的关系,只不过集合的定义由二进制表示变成了素数分解
我们换一种写法
\(\forall 1\leq i\leq n\),求\(∑_{j|i}a_j\)
我们只要按照埃氏筛的样子做一遍更新就可以了
1
2
3
4
5
6
7
| for(int i=1;i<=n;++i)
{
if(!vis[i])
{
for(int j=1;j*i<=n;++j) sum[i*j]+=sum[j],vis[i*j]=1;
}
}
|
如果要预处理的话也可以,唯一需要注意的,跟上文一样,这里我们的维度是由不同的素因子来确定的,所以我们要先枚举素因子来保证每一维的前缀和都更新全了
1
2
3
4
5
6
7
| for(int i=1;i<=totprime;++i)
{
for(int j=1;p[i]*j<=n;++j)
{
sum[p[i]*j]+=sum[j];
}
}
|
那么这种东西其实有一种更加正式的名字:
狄利克雷前缀和
Dirichlet 前缀和
大意:如上
思路:如上
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #include<bits/stdc++.h>
using namespace std;
#define ll unsigned int
#define endl '\n'
const ll N=2e7+10;
ll n,a;
ll seed;
inline ll getnext(){
seed^=seed<<13;
seed^=seed>>17;
seed^=seed<<5;
return seed;
}
ll b[N];
bool vis[N];
ll ans=0;
void solve()
{
cin>>n>>seed;
for(int i=1;i<=n;++i) b[i]=getnext();
vis[1]=1;
for(int i=1;i<=n;++i)
{
if(!vis[i])
{
for(int j=1;j*i<=n;++j) b[i*j]+=b[j],vis[i*j]=1;
}
}
for(int i=1;i<=n;++i) ans^=b[i];
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}
|
事实上还有一种东西叫做
狄利克雷后缀和
\(∀1≤i≤n,求∑_{i|j}a_j\)
其实也不难理解,就是素因子分解下的枚举超集的后缀和,跟上面讲的二进制超集后缀和一个意思
1
2
3
4
5
6
7
| for(int i=1;i<=totprime;++i)
{
for(int j=n/p[i];j;--j)
{
sum[j]+=sum[j*p[j]];
}
}
|
但是因为这里我们需要用到比自己大的值,所以内层需要倒序更新
cf 757 D2. Divan
and Kostomuksha (hard version)
大意: 给定一个数组\(a\),要求重排数组,使得数组的前缀\(gcd\)之和最大
思路: 一个显然的小贪心:如果一开始的\(gcd\)是\(x\)的话,我们一定要尽可能多的保留\(gcd\)为\(x\),因为后面的\(gcd\)不会大于\(x\)。要做到这一点,我们需要统计有多少个数字是\(x\)的倍数
换句话说,我们需要统计\(cnt_i\),表示有多少个数字是\(i\)的倍数,这其实就是一个狄利克雷后缀和
这里还有一个性质:\(cnt_j\)一定不大于\(cnt_i\),这一点显然
那么我们如果以\(i\)作为一开始的\(gcd\)的话,会保留\(cnt_i\)个前缀\(gcd\)为\(i\)的长度,如果以\(j\)作为一开始的\(gcd\)的话,会保留\(cnt_j\)个前缀\(gcd\)为\(j\)的长度,这个长度肯定是不大于上一个的,所以我们可以从\(i\)转移到\(j\),
设\(dp_i\)表示一开始的\(gcd\)为\(i\)的情况下数组的最大价值
\(dp_j=max(dp_j,1ll*cnt_j*(j-i)+dp_i);\)
一开始的初始条件是\(dp_1=1\)
另外这题数据范围有点大,需要预处理一下素数,然后按素数转移即可
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| #include<bits/stdc++.h>
using namespace std;
#define ll int
#define endl '\n'
const ll N=2e7;
ll n,a;
ll cn=0;
ll cnt[N+10];
long long dp[N+10];
ll p[N+10];
bool vis[N+10];
void init()
{
for(int i=2;i<=N;++i)
{
if(!vis[i])
{
p[++cn]=i;
}
for(int j=1;j<=cn&&i*p[j]<=N;++j)
{
vis[i*p[j]]=1;
if(i%p[j]==0) break;
}
}
}
void solve()
{
init();
cin>>n;
for(int i=1;i<=n;++i)
{
cin>>a;
cnt[a]++;
}
for(int i=1;i<=cn;++i)
{
for(int j=N/p[i];j;--j)
{
cnt[j]+=cnt[j*p[i]];
}
}
dp[1]=n;
long long ans=0;
for(int i=1;i<=N;++i)
{
for(int j=1;i*p[j]<=N;++j)
{
ll sd=i*p[j];
dp[sd]=max(dp[sd],1ll*cnt[sd]*(sd-i)+dp[i]);
}
ans=max(ans,dp[i]);
}
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
|

