基于决策单调性的dp优化
对于决策单调性的一般解释
对于一个常见的一维\(dp:dp_i=min/max\{dp_j+w(j,i)\}\),显然每一个点的dp值只能从\(\{j|j<i\}\)的\(dp_j\)转移而来,我们记每一个点\(i\)的最优决策转移点为\(p_i\).如果我们从1-n遍历i,\(p_i\)也随之单调变化,那么这个dp就具有决策单调性了.大部分决策单调性体现在决策点单调递增,但是也有决策点单调递减的情况(都是建立在枚举的点是从小到大的情况下)
关于决策单调性的证明
该部分讲解如无特殊声明,都是建立在求最小化问题的基础上,如果要求最大化的话,将对应不等号取反即可
四边形不等式
一维dp
对应方程形式\(F\) :\(\large
dp_i=min_{j<i}\{dp_j+w(j,i)\}\)
我们考虑\(p_1\leq p_2\leq p_3\leq
p_4\)
则最小化情况下的四边形不等式表示为:\(w(p_1,p_3)+w(p_2,p_4)\leq
w(p_1,p_4)+w(p_2,p_3)\)
特别的,如果等号永远成立,称为四边形恒等式
一般记为:交叉\(\leq\)包含
定理1:如果对于dp式F,其w满足四边形不等式,则F满足决策单调性
\(Proof:\)
反证法。记\(dp_i\)的最优决策点为\(p_i\),假设\(y<x\)且\(p_x<p_y\).根据\(F\)的定义有:\(dp_x=dp_{p_x}+w(p_x,x)\leq
dp_{p_y}+w(p_y,x)(1)\)
不难发现\(p_x<p_y<y<x\),故由四边形不等式:\(w(p_x,y)+w(p_y,x)\leq
w(p_x,x)+w(p_y,y)(2)\)
\(1,2\)两式相加得到:\(dp_{p_x}+w(p_x,y)\leq
dp_{p_y}+w(p_y,y)\)
则对于\(y\)来说,\(p_x\)是一个比\(p_y\)更优的决策点,与条件矛盾。
故\(y<x\)意味着\(p_y\leq p_x\),单调性得证
区间dp
一般来说高维dp的决策单调性体现在某一个维度,相对一维dp来说也会更加难发现,但是一种区间dp具有较好的性质
对应方程形式\(F\) \(\large
:dp_{i,j}=min_{k=i}^{j-1}\{dp_{i,k}+dp_{k+1,j}+w(i,j)\}\)
这里先介绍一个跟四边形不等式非常像的区间包含不等式:考虑\(p_1\leq p_2\leq p_3\leq p_4\),则\(w(p_1,p_4)\geq w(p_2,p_3)\)
引理1:如果对于dp式F,其w同时满足四边形不等式以及区间包含不等式,则F也满足四边形不等式
定理2:如果对于dp式F,其满足四边形不等式,记\(p_{i,j}为dp_{i,j}\)的最优决策点,则\(\forall i<j,p_{i,j-1}\leq p_{i,j}\leq
p_{i+1,j}\)
基于此,我们对于\(F\)就能给出一个复杂度为\(O(n^2)\)的优化。
如果在计算\(f_{i,j}\)的同时记录\(p_{i,j}\),则对决策点\(K\)的枚举量为\(\sum_{1\leq i<j\leq n}p_{i+1,j}-p_{i,j-1}=
\sum_{i=1}^{n}p_{i,n}-p_{1,i}\leq n^2\)
例题:
HDU Monkey
Party
HDU Tree
Construction
这里给出Monkey Party的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2020;
ll n;
ll mas[N];
ll dp[N][N];
ll s[N][N];
ll sum[N];
ll w(ll l,ll r)
{
return sum[r]-sum[l-1];
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
while(cin>>n)
{
for(int i=1;i<=n;++i) cin>>mas[i];
for(int i=1+n;i<=n+n;++i) mas[i]=mas[i-n];
for(int i=1;i<=n+n;++i) sum[i]=sum[i-1]+mas[i];
memset(dp,0x3f,sizeof dp);
for(int i=0;i<=n+n;++i) dp[i][i]=0,s[i][i]=i;
for(int len=2;len<=n;len++){
for(int i=1;i<=2*n-len+1;i++){
int j=i+len-1;
for(int k=s[i][j-1];k<=s[i+1][j];k++){
if(dp[i][j]>dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]){
dp[i][j]=dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1];
s[i][j]=k;
}
}
}
}
ll ans=1e17;
for(int l=1;l<=n;++l)
{
ans=min(ans,dp[l][l+n-1]);
}
cout<<ans<<endl;
}
return 0;
}
|
一种二维dp
这一块存疑
也是一种非常常见的dp式\(f\) \(:dp_{i,j}=min_{k<i}\{dp_{k,j-1}+w(k,i)\}\)
理论上它与上一块的区间dp是不同类型的,但是仿佛只要\(w\)满足引理1,\(F\)也有同样的结论。我没看到过严格证明,OIWIKI上也没找到对应介绍,但是大家好像都默认这是正确的,而且本人目前没找到反例
反正用定理2来优化该dp的话,时间复杂度是\(O(n^2)\)的
例题:
HDU
Division
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| #include<bits/stdc++.h>
using namespace std;
#define ll int
const ll N=10005;
ll t,n,m;
ll dp[N][5010];
ll mas[N];
ll f(ll l,ll r)
{
return (mas[r]-mas[l])*(mas[r]-mas[l]);
}
ll d[N][5010];
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>t;
for(int s=1;s<=t;++s)
{
cin>>n>>m;
for(int i=1;i<=n;++i) cin>>mas[i];
sort(mas+1,mas+1+n);
memset(dp,0x3f,sizeof dp);
dp[0][0]=0;
for(int j=1;j<=m;++j)
{
d[n+1][j]=n;
for(int i=n;i;--i)
{
ll tmp=0x3f3f3f3f;
ll p;
for(int k=d[i][j-1];k<=d[i+1][j];++k)
{
if(tmp>dp[k][j-1]+f(k+1,i))
{
tmp=dp[k][j-1]+f(k+1,i);
p=k;
}
}
dp[i][j]=tmp;
d[i][j]=p;
}
}
cout<<"Case "<<s<<": "<<dp[n][m]<<endl;
}
return 0;
}
|
一些满足四边形不等式的函数类
- 若\(w_{1(i,j)},w_{2(i,j)}\)均满足四边形不等式(或区间包含不等式),则\(\forall c_1,c_2\geq 0\),\(c_1w_{1(i,j)}+c_2w_{2(i,j)}\)也对应地满足四边形不等式(或区间包含不等式)
- 若存在函数\(f,g\),使得\(w_{l,r}=f_r-g_l\),则\(w\)满足四边形恒等式(等号永远成立)。当\(f,g\)单调增的时候,\(w\)还满足区间包含不等式
- 设\(h_x\)是一个单调增的下凸函数,若\(w\)满足四边形不等式以及区间包含不等式,则\(h(w(x))\)也满足四边形不等式以及区间包含不等式
- 设\(h_x\)是一个下凸函数,若\(w\)满足四边形恒等式以及区间包含不等式,则\(h(w(x))\)满足四边形不等式
具体证明详见OIWIKI
这里以NOI 2009
诗人小G的dp递推式来试着用这些结论证一下决策单调性
\(dp_i=min_{0\leq
j<i}\{dp_j+|s_i-s_j-1-L|^P\}\),其中\(s_i=i+\sum_{k=1}^{i}a_k\),\(a_k>0\)为常值
这里\(w_{j,i}=|s_i-s_j-1-L|^P\),我们不妨记\(m_{j,i}=s_i-s_j-1-L\),则\(w_{j,i}=|m_{j,i}|^P\)
我们考虑利用第2条结论:记\(f_i=s_i-1-L,g_i=s_i\),显然\(m_{j,i}=f_i-g_j\),故\(m_{j,i}\)满足四边形不等式,又\(f_i,g_i\)显然单增,故\(m_{j,i}\)满足区间包含不等式
又函数\(|x|^P\)显然是一个下凸函数,故由第4条结论可知,\(w_{j,i}=m_{j,i}\)也满足四边形不等式。再由定理1,该dp式满足决策单调性。证毕。
可以看到如果式子能记住的话,在面对一些比较复杂的递推式的时候能够较从容地推出决策单调性,如果直接用四边形不等式的定义硬证这题的话,还是需要不少分类讨论和强大的推柿子能力的(啊...只会套公式的屑)
与图形相结合
来自一位大佬的奇妙讨论,从另一个视角帮助我们理解了决策单调性
这里讨论一维最优化dp,也就是\(F\)
\(:dp_i=min_{j\leq
i}\{dp_j+w(j,i)\}\)
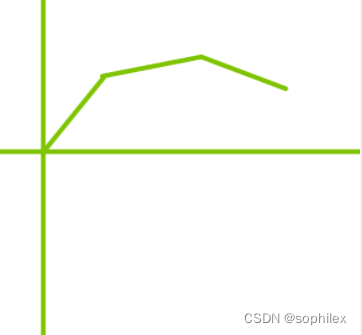
决策单调性意味着决策点是单调的,换句话说,每一个点能够作为最优决策点的范围是一段连续区间
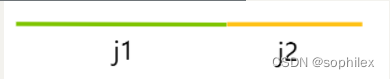
在绿色区间内的点都是被\(dp_{j_1}\)更新,在黄色区间内的点都是被\(dp_{j_2}\)更新,不会出现黄色区间内有某个点是被\(dp_{j_1}\)更新的情况,否则就违背了决策单调性的定义
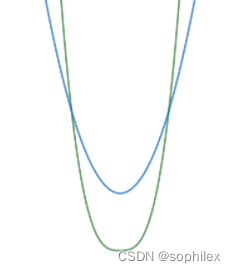
从几何视角来看这一事实。我们考虑\(g_j(i)\),表示\(dp_j+w(j,i)\),则\(dp_i\)可以重新表示为\(dp_i=min_{j\leq
i}\{g_j(i)\}\)。我们可以将\(g_j(i)\)看成\(j\)为常值,\(i\)为自变量的一个函数,那么\(dp_i\)本质上就是在所有函数\(g_j(i)\)里取最小值来转移
还是以上图为例,绿色区间内的点对应函数\(g_{j_1}(i)\),黄色区间内对应函数\(g_{j_2}(i)\),我们可以得到一个结论:两个函数只能有一个交点,否则就会出现前一段是\(g_{j_1}(i)\)更小,中间是\(g_{j_2}(i)\),后面又变成\(g_{j_1}(i)\)更小的局面,那就违背了决策单调性的定义。反过来,如果只有一个交点的话,这两段区间就满足决策单调性
整体来看,我们可以得到:如果所有\(g_j(i)\)两两之间都至多只有一个交点的话,\(F\)是满足决策单调性的。个人感觉该命题的逆命题并不成立,毕竟实际在转移的时候只用考虑最小值的变化,值较大的函数之间是如何纠缠的我们并不关系。所以该结论应该只适用于证明决策单调性,而不能证否决策单调性
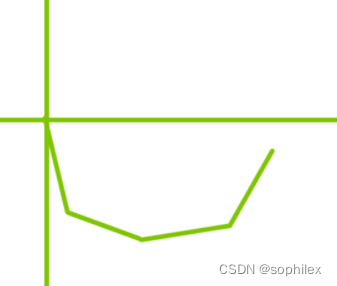
接下来我们考虑,如果\(g_j(i)\)之间至多只有一个交点,需要满足什么性质
该大佬给出的两个条件是:
- \(g_j(i)\)之间可以通过平移相互变换
- \(g_j(i)\)的导函数在定义域内单调增/减(凸性唯一)
以下分别是不满足对应条件的反例
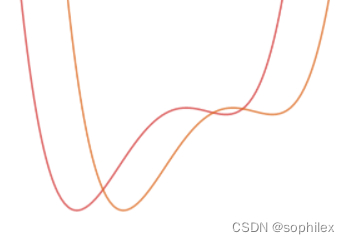
这两个条件不一定充分,只是感觉上可能也够了
然后大佬给出的一些总结:
具体怎么用单调栈,单调队列,我会在后面有所涉及
决策单调性的常见优化手段
二分队列
这应该算是最常见的一种利用决策单调性来优化dp的手段了。它只能用于决策点单调增的情况。
考虑之前的一个结论:每一个决策点的更新范围是一段连续区间。这意味着相邻两个决策点的更新范围之间存在着一个分界线\(K\),当\(i<=k\)的时候,由前一个点\(j_1\)更新,之后就由后一个点\(j_2\)更新,并且\(j_1\)就再也没有机会了。那么我们就可以维护一个单调队列来实现每次\(O(logn)\)的更新
具体来说,我们的单调队列中的每一个元素是一个三元组\(\{P,l_p,r_p\}\),分别表示当前的决策点\(P\),它能更新区间的左界\(l_p\),它能更新区间的右界\(r_p\)。那么当我们尝试更新\(dp_i\)的时候,
弹出队头。因为队列里的点的对应决策区间是单调的,所以我们可以直接将\(r_p<i\)的队头三元组不断弹出。
用队头的\(P\)更新\(dp_i\)
将三元组\(\{i,l_i,r_i\}\)放入队列尾部。那么怎么求\(l_i,r_i\)?在求\(l_i\)之前,我们要意识到一个事实:我们所求的\(l_p,r_p\)都是建立在已经遍历到的点的信息上而建立的,换句话说,随着后面新的点\(i\)加入,它的决策区间有可能会完全包含某一个点\(P\)的决策区间。这一点很好理解:原本\(l_i,r_i\)就是由\(i\)更新的,但是因为我们还没有遍历到\(i\),所以这段区间就会先被其它点占据。所以我们在求\(l_i\)之前,要先将队尾那些完全不会比\(i\)优的点踢出。具体如何判断?我们只要看一下在\(l_p\)处\(i\)是否比\(P\)更优即可。如果是,显然\(P\)就再也没有机会比\(i\)更优了,因为\(p<i\)。
该操作之后\(i\)就不能将队尾的\(P\)的区间完全覆盖了,我们就可以利用单调性二分一下两者的决策区间的边界,作为\(l_i\).至于\(r_i\),我们直接设成\(n\)即可。毕竟此时后面的点还没加入,我们只能用\(i\)来更新它们。
贴个模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| void Optimize()
{
hd=1,tl=0;
que[++tl]=0;ls[0]=1,rs[0]=n;
for(int i=1;i<=n;++i)
{
while(hd<tl&&rs[que[hd]]<i) hd++;
dp[i]=cal(que[hd],i);
while(hd<tl&&cal(i,ls[que[tl]])<=cal(que[tl],ls[que[tl]])) tl--;
ll l=ls[que[tl]],r=n+1;
while(l<=r)
{
ll mid=(l+r)>>1;
if(cal(i,mid)<=cal(que[tl],mid)) r=mid-1;
else l=mid+1;
}
p_ans=r+1;
if(p_ans>n) continue;
rs[que[tl]]=p_ans-1;
que[++tl]=i;
ls[i]=p_ans,rs[i]=n;
}
}
|
Tips:二分决策区间边界的时候,右界设置为n+1,因为i有可能完全不如P优,要防一手
如果\(w(j,i)\)我们能够以\(O(1)\)的复杂度求出的话,该方法的时间复杂度式\(O(nlog)\)的
例题:
NOI 2009
诗人小G
dp式并不难列出,关于其决策单调性我们已经在上一块里证明过了,所以这里直接用二分队列即可
数据范围有点大,记得开long double
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ld long double
#define IL inline
#define endl '\n'
const ll N=100010;
const ll mod=998244353;
const ll inf=1e18;
inline int read()
{
int X=0; bool flag=1; char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}
while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}
if(flag) return X;
return ~(X-1);
}
int n,L,P;
char s[N][50];
ld mas[N];
int ls[N],rs[N],pre[N];
int que[N];
int hd,tl,p_ans;
ld dp[N];
ld ksm(ld x,ll y)
{
ld ans=1;
while(y)
{
if(y&1) ans=ans*x;
x=x*x;
y>>=1;
}
return ans;
}
ld cal(ll k,ll x)
{
return dp[k]+ksm(abs(mas[x]-mas[k]-1-L),P);
}
void solve()
{
n=read();L=read();P=read();
for(int i=1;i<=n;++i) scanf("%s",s[i]);
for(int i=1;i<=n;++i)
{
mas[i]=mas[i-1]+strlen(s[i])+1;
}
hd=1,tl=0;
que[++tl]=0;ls[0]=1,rs[0]=n;
for(int i=1;i<=n;++i)
{
while(hd<tl&&rs[que[hd]]<i) hd++;
dp[i]=cal(que[hd],i);
pre[i]=que[hd];
while(hd<tl&&cal(i,ls[que[tl]])<=cal(que[tl],ls[que[tl]])) tl--;
ll l=ls[que[tl]],r=n+1;
while(l<=r)
{
ll mid=(l+r)>>1;
if(cal(i,mid)<=cal(que[tl],mid)) r=mid-1;
else l=mid+1;
}
p_ans=r+1;
if(p_ans>n) continue;
rs[que[tl]]=p_ans-1;
que[++tl]=i;
ls[i]=p_ans,rs[i]=n;
}
if(dp[n]>inf)
{
puts("Too hard to arrange");
}
else
{
printf("%lld\n",(ll)dp[n]);
vector<string> ans;
ll pos=n;
while(1)
{
ll x=pre[pos]+1;
string ss="";
for(int i=x;i<pos;++i) ss+=s[i],ss+=" ";
ss+=s[pos];
ans.push_back(ss);
pos=pre[pos];
if(pos==0) break;
}
reverse(ans.begin(),ans.end());
for(auto i:ans) cout<<i<<endl;
}
puts("--------------------");
}
int main()
{
ll t;t=read();while(t--)
solve();
return 0;
}
|
二分栈
一般用于最优决策点是不增的情况。在原本的二分队列的做法中,我们从队列的首部取出最优决策点,从队列的尾部放入决策点。那么如果决策点是不增的,意味着我们需要从队列的尾部取最优决策点。这样取和放的操作都是在队列的尾部,我们只要用一个栈来实现就好了。同样的,相邻的两个决策点更新的区间会有一个边界,我们不妨记为\(k_{l,r}\),当尝试加入\(i\)的时候,记队列倒数第一个元素为\(p_1\),倒数第二个元素为\(p_2\),那么如果\(k_{p_1,p_2}\leq k_{p_2,i}\),那么\(p_2\)就可以踢掉了,因为它不管在什么时候都不会是\(i,p_1,p_2\)中的最优解。然后将\(i\)加入队列之后再按照\(k_{p_1,p_2}\)是否\(\leq i\)来踢即可
JSOI2001
柠檬
思路:
首先不难发现最优选择下每一段的首尾的颜色就是这段的\(s_0\),否则我们就可以将首尾的没用的点分出去自称一段,贡献一定更优
所以我们可以按照不同的颜色来分开处理
\(dp_i=max_{col_j=col_i,j\leq
i}\{dp_{j-1}+w(j,i)\}\),其中\(w(j,i)=(sum_i-sum_j+1)^2\)
这里我们画图就能发现决策点是单调不增的(按照上文与图形结合的方法),所以可以使用二分栈。但是这题的决策单调性是在相同颜色的点之间才存在的,所以我们要分开来做二分栈
然后每一个点不会从0转移,所以一开始也不用把0放进去
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| #include <bits/stdc++.h>
#define pii pair<int,int>
#define il inline
#define ll long long
using namespace std;
#define bc(idx) vt[idx].size()-1
#define bd(idx) vt[idx].size()-2
#define g(a,b) vt[a][b]
const int N=200000;
const ll inf=1e18;
ll n;
ll mas[N];
vector<ll> vt[N];
ll dp[N];
ll ls[N],rs[N];
map<ll,ll> mp;
ll sum[N];
ll gt(ll k,ll num)
{
return dp[k-1]+mas[k]*num*num;
}
ll gtf(ll a,ll b)
{
ll l=1,r=n;
while(l<=r)
{
ll mid=l+r>>1;
if(gt(a,mid-sum[a]+1)>=gt(b,mid-sum[b]+1)) r=mid-1;
else l=mid+1;
}
return r+1;
}
void solve()
{
cin>>n;
for(int i=1;i<=n;++i)
{
cin>>mas[i];
mp[mas[i]]++;
sum[i]=mp[mas[i]];
}
for(int i=1;i<=n;++i)
{
ll idx=mas[i];
while(vt[idx].size()>=2&& gtf(g(idx,bd(idx)),g(idx,bc(idx)))<=gtf(g(idx,bc(idx)),i)) vt[idx].pop_back();
vt[idx].push_back(i);
while(vt[idx].size()>=2&& gtf(g(idx,bd(idx)),g(idx,bc(idx)))<=sum[i]) vt[idx].pop_back();
dp[i]=gt(g(idx,bc(idx)),sum[i]-sum[g(idx,bc(idx))]+1);
}
cout<<dp[n]<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}
|
分治
分治的方法主要用于同一层之间的点相互之间线性无关的情况。
比如\(F_1\) \(:dp_{i,j}=min\{dp_{i-1,k}+w(k,i)\}\).\(F_2\) \(:dp_i=min\{a_k+w(k,i)\}\)
可以看到同一层之间的点不会相互转移
那么如果同一层的点满足决策单调性的话,也就是意味着决策点是单调的,我们就可以采用分治的策略来优化转移的过程
假设当前需要转移的区间是\([L,R]\),决策点的选择区间是\([p_l,p_r]\)(显然一开始转移区间和决策点的选择区间都为\([1,n]\)),设\(mid=\frac{L+R}{2}\),我们可以先暴力求出\(mid\)的最优决策点\(pos\),那么\([L,mid-1]\)的决策点选择区间就是\([p_l,pos]\),\([mid+1,R]\)的决策点选择区间就是\([pos,p_r]\),那么这样分治下去就好了。
如果我们可以\(O(1)\)求代价的话,对\(mid\)求\(pos\)的时间复杂度就只有\(O(n)\),再加上每次要处理的区间长度会变成原本的一半,所以处理区间为n的复杂度是\(f(n)=O(n)+O(f(n/2))\),总复杂度是\(O(nlogn)\)
一个板子:
1
2
3
4
5
6
7
8
9
10
11
12
13
| void Solve(ll l,ll r,ll pl,ll pr)
{
ll mid=l+r>>1;
ll pos;
dp[mid]=gt(pos=pl,mid);
for(int i=pl+1;i<=min(mid-1,pr);++i)
{
if(gt(i,mid)<dp[mid]) dp[mid]=gt(pos=i,mid);
}
if(l<mid) Solve(l,mid-1,pl,pos);
if(r>mid) Solve(mid+1,r,pos,pr);
}
|
JSOI2016
灯塔
大意:
给定\(h_i\),对于每一个\(i\),要求\(\forall
j,p_i\geq h_j-h_i+\sqrt{|i-j|}\),求最小的\(p_i\)
思路:
不妨先将绝对值去掉,那么\(p_i=\left\{\begin{matrix}
min\{h_j+\sqrt{i-j}-h_i\} & j<i\\ min\{h_j+\sqrt{j-i}-h_i\} &
j>i \end{matrix}\right.\)
那么我们只要处理第一个式子就好了,第二个式子只要把整个数组反一下即可
可以发现\(p_i=min\{h_j+\sqrt{i-j}-h_i\}\)满足决策单调性,并且\(p_i\)之间相互无关,所以直接分治就解决了
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
#define IL inline
#define endl '\n'
const ll N=5e5+10;
double ep=1e-9;
const ll mod=998244353;
const ll inf=1e18;
ll n;
ll mas[N];
double dp1[N],dp2[N];
double gt(ll p,ll x)
{
return mas[p]+sqrt(x-p)-mas[x];
}
void Solve(ll l,ll r,ll pl,ll pr,double *dp)
{
ll mid=(l+r)>>1;
ll pos=pl;
for(int i=pl;i<=min(mid,pr);++i)
{
if(gt(i,mid)-dp[mid]>=-ep) dp[mid]=gt(pos=i,mid);
}
if(l<mid) Solve(l,mid-1,pl,pos,dp);
if(r>mid) Solve(mid+1,r,pos,pr,dp);
}
void solve()
{
cin>>n;
for(int i=1;i<=n;++i) cin>>mas[i];
Solve(1,n,1,n,dp1);
reverse(mas+1,mas+1+n);
Solve(1,n,1,n,dp2);
for(int i=1;i<=n;++i)
{
double x=fmax(dp1[i],dp2[n-i+1]);
cout<<(ll)ceil(x)<<endl;
}
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}
|
SDOI2016
征途
CF321 E
类莫队做法
注意到分治要保证时间复杂度的前提是每次求\(w\)代价的复杂度是\(O(1)\)的
但是有一类\(w\)比较特殊:关于区间的信息的记录,比如区间数字种类数等。这种问题我们一般可以离线下来用莫队处理,那么仿照莫队用左右端点的连续移动就可以做到\(O(1)\)转移了,因为我们的决策点的选择范围也刚好是一个连续的区间,所以这样的话复杂度是正确的
CF868 F
CmdOI2019
任务分配问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
| #include<bits/stdc++.h>
#include <iostream>
using namespace std;
#define ll int
#define IL inline
#define endl '\n'
const ll N=3e4+10;
double ep=1e-9;
const ll mod=998244353;
const ll inf=1e9;
struct Tree
{
ll tr[N];
#define low(x) x&(-x)
void add(ll x,ll y)
{
while(x<N)
{
tr[x]+=y;
x+=low(x);
}
}
ll sum(ll x)
{
ll ans=0;
while(x)
{
ans+=tr[x];
x-=low(x);
}
return ans;
}
}T;
ll n,k;
ll mas[N];
ll dp[N],pp[N];
namespace Mo
{
int L=1,R=0;
ll ans=0;
int col[N];
ll cnt[N];
void add1(ll pos,ll op)
{
if(op==1)
{
ans+=T.sum(n+1)-T.sum(col[pos]);
T.add(col[pos],1);
}
else
{
ans-=T.sum(n+1)-T.sum(col[pos]);
T.add(col[pos],-1);
}
}
void add2(ll pos,ll op)
{
if(op==1)
{
ans+=T.sum(col[pos]-1);
T.add(col[pos],1);
}
else
{
ans-=T.sum(col[pos]-1);
T.add(col[pos],-1);
}
}
ll gt(ll l,ll r)
{
l++;
while(L<l) add1(L++,0);
while(L>l) add1(--L,1);
while(R>r) add2(R--,0);
while(R<r) add2(++R,1);
return pp[l-1]+ans;
}
}
void Solve(ll l,ll r,ll pl,ll pr)
{
ll mid=(l+r)>>1;
ll pos;
dp[mid]=Mo::gt(pos=pl,mid);
for(int i=pl+1;i<=min(mid-1,pr);++i)
{
if(dp[mid]>Mo::gt(i,mid)) dp[mid]=Mo::gt(pos=i,mid);
}
if(l<mid) Solve(l,mid-1,pl,pos);
if(r>mid) Solve(mid+1,r,pos,pr);
}
void solve()
{
cin>>n>>k;
for(int i=1;i<=n;++i)
{
cin>>Mo::col[i];
}
for(int i=1;i<=n;++i) pp[i]=Mo::gt(0,i);
for(int i=1;i<k;++i)
{
Solve(1,n,0,n);
for(int j=1;j<=n;++j) pp[j]=dp[j];
}
cout<<pp[n]<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}
|
SMAWK
SMAWK的用途跟分治一样,用于处理同一层之间没有转移关系的情况,但是复杂度会更优,可以达到\(O(n)\)
我们考虑从另一个角度来理解决策单调性
定义1
若矩阵A满足∀i,j∈[0,k],pos(i)<pos(j)则称A为单调矩阵。若A的任意子矩阵均为单调矩阵,则称A为完全单调矩阵
重新定义四边形不等式
定义2 对于n*m的矩阵A,若\(\forall
1<i_1<i_2\leq n,1\leq j_1,\leq j_2\leq m\),均有\(A_{i_1,j_1}+A_{i_2,j_2}\leq
A_{i_1,j_2}+A_{i_2,j_1}\),则称A满足四边形不等式
快速判断矩阵是否满足四边形不等式:
定理1 对于n*m的矩阵A,若\(\forall
1<i<n,1\leq j<m\),均有\(A_{i,j}+A_{i+1,j+1}\leq
A_{i,j+1}+A_{i+1,j}\),则称A满足四边形不等式
定理2 若矩阵A满足四边形不等式,则A以及\(A^{T}\)是完全单调矩阵
接下来考虑\(dp_i=min_{j<i}\{a_j+w(j,i)\}\),放到矩阵上,当\(j<i\)时,\(A_{i,j}=dp_j+w(j,i),j\geq i\)时,令\(A_{i,j}=inf\),那么求\(dp_i\)其实就是在第i行找最小值对应的列j.如果矩阵是一个单调矩阵,也就是dp满足决策单调性,我们就可以采用SMAWK
SMAWK的核心内容是reduce的过程,当列数m远大于n的时候,我们的枚举量会多很多,但是其实一行只会对应一个最优列,所以大量列是多余的,reduce过程就是在去除这些冗余列
当然,为了保证一行只有一个答案,我们要限定取每一行最左边/最右边的最小值(这一点在与WQS二分结合的时候很重要)
其步骤如下:
1初始定义 k = 1;
2当 n ≥ m 时结束过程;否则比较 \(A_{k,k}\) 和 \(A_{k,k+1}\)
3若 \(A_{k,k}\geq
A_{k,k+1}\),删除第 k 列,k ←
max(k − 1, 1),回到步骤 2;
4若 \(A_{k,k}< A_{k,k+1}\) 且
k = n,删除第 n + 1 列,回到步骤 2;
5若 \(A_{k,k}< A_{k,k+1}\) 且
k = n,k ← k + 1,回到步骤
2。
每一步的原因还是很显然的,这里不多赘述了。复杂度是\(O(m+n)\)
为了保证线性复杂度的正确性,可以用链表实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
| struct Node
{
ll val,opt;
Node *lst,*nxt;
Node(){val=opt=0;lst=nxt=NULL;}
};
struct List
{
ll len;
Node *s,*e;
List()
{
len=0;
s=new Node();s->opt=1;
e=new Node();e->opt=-1;
s->nxt=e;e->lst=s;
}
void append(ll x)
{
Node *n=new Node();
n->val=x;
Node *a=e->lst;
a->nxt=n;n->lst=a;
n->nxt=e;e->lst=n;
len++;
}
List(const List &a)
{
len=0;
s=new Node();s->opt=1;
e=new Node();e->opt=-1;
s->nxt=e;e->lst=s;
Node *n=a.s->nxt;
while(n->opt!=-1)
{
append(n->val);
n=n->nxt;
}
}
Node* del(Node *n)
{
--len;
Node *a=n->lst,*b=n->nxt;
a->nxt=b,b->lst=a;
delete(n);
return a;
}
};
struct submat
{
List r,c;
}A;
submat Reduce(const submat &A)
{
submat B;
B.r=(List)A.r;B.c=(List)A.c;
int n=A.r.len;
int m=A.c.len;
Node *nr=B.r.s->nxt;
Node *nc=B.c.s->nxt;
ll k=1;
while(n<m)
{
if(get(nr->val,nc->val)>get(nr->val,nc->nxt->val))
{
nc=B.c.del(nc);
m--;
if(k>1)
{
--k;
nr=nr->lst;
}
else
{
nr=B.r.s->nxt;nc=B.c.s->nxt;
}
}
else if(k==n)
{
B.c.del(nc->nxt);m--;
}
else
{
k++;
nr=nr->nxt;nc=nc->nxt;
}
}
return B;
}
|
reduce之后我们就真正开始SMAWK了
SMAWK(A) 表示计算 n × m 的完全单调矩阵
A 的每行最小值所在
列。步骤如下:
- 1若 min(n, m) = 1 直接计算答案;
- 2对Areduce,得到矩阵B,并且我们取其所有偶数行组成一个新矩阵C
- 4递归SMAWK(C),得到C的每一行的最小值所在位置
- 4对于B中的奇数行,其答案在相邻两行的答案之间,那么之间暴力遍历一下即可。该步骤的复杂度为\(O(m)\)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| void SMAWK(submat A)
{
int n=A.r.len;
int m=A.c.len;
if(n==1)
{
ll x=A.r.s->nxt->val;
Node *nc=A.c.s->nxt;
ll maxn=0;
ll maxp=0;
while(nc->opt!=-1)
{
if(get(x,nc->val)>=maxn)
{
maxp=nc->val,maxn=get(x,nc->val);
}
nc=nc->nxt;
}
ans[x]=maxp;
return;
}
if(m==1)
{
ll y=A.c.s->nxt->val;
Node *nr=A.r.s->nxt;
while(nr->opt!=-1)
{
ans[nr->val]=y;
nr=nr->nxt;
}
return;
}
submat B=Reduce(A);
submat C;C.c=List(B.c);
Node *nr=B.r.s->nxt;
bool fl=0;
while(nr->opt!=-1)
{
if(fl) C.r.append(nr->val);
nr=nr->nxt;
fl^=1;
}
SMAWK(C);
nr=B.r.s->nxt;fl=0;
Node *nc=B.c.s->nxt;
while(nr->opt!=-1)
{
if(!fl)
{
ll z=ans[nr->nxt->val];
ll x=nr->val;
ll maxn=0,maxp=0;
if(z==0) z=inf;
while(nc->opt!=-1 && nc->val<=z)
{
if(get(x,nc->val)>=maxn)
{
maxn=get(x,nc->val);
maxp=nc->val;
}
nc=nc->nxt;
}
if(nc->lst->val==z) nc=nc->lst;
ans[x]=maxp;
}
nr=nr->nxt;
fl^=1;
}
}
|
理论上是可以平替分治的,但是写起来太烦了。。。
有一份短一点的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
|
int pre[N],suf[N],M[N],n,m,ans=1e18,P=0;
vector<int>L,H;
map<int,int>Mp[N];
ll get(ll a,ll b)
{
}
int pre[N],suf[N],M[N],P=0;
void del(int x)
{
if (pre[x]!=-1)
suf[pre[x]]=suf[x]; else P=suf[x];
pre[suf[x]]=pre[x];
}
vector<int> reduce(vector<int>X,vector<int>Y)
{
for (int i=0;i<Y.size();i++) pre[i]=i-1,suf[i]=i+1;
int x=0,y=0;
P=0;
for (int nmsl=Y.size()-X.size();nmsl>0;nmsl--)
{
if (get(X[x],Y[y])<get(X[x],Y[suf[y]]))
{
y=suf[y];
del(pre[y]);
if (x) y=pre[y],x--;
} else
{
if (x==X.size()-1) del(suf[y]);
else
{
y=suf[y];
x++;
}
}
}
vector<int>ret;
for (int i=P;i!=Y.size();i=suf[i]) ret.push_back(Y[i]);
return ret;
}
void Solve(vector<int>X,vector<int>Y)
{
Y=reduce(X,Y);
if (X.size()==1)
{
M[X[0]]=Y[0];
return;
}
vector<int>Z;
for (int i=0;i<X.size();i++)
if (!(i%2)) Z.push_back(X[i]);
Solve(Z,Y);
for (int i=0;i<X.size();i++)
{
if (!(i%2)) continue;
int l=lower_bound(Y.begin(),Y.end(),M[X[i-1]])-Y.begin();
int r=0;
if (i==X.size()-1) r=Y.size()-1;
else
{
r=lower_bound(Y.begin(),Y.end(),M[X[i+1]])-Y.begin();
}
M[X[i]]=Y[l];
while (l<r)
{
l++;
if (get(X[i],Y[l])>get(X[i],M[X[i]])) M[X[i]]=Y[l];
}
}
}
signed main()
{
cin>>n>>m;
for (int i=1;i<=n;i++)
{
H.push_back(i);
}
for (int i=1;i<=m;i++) L.push_back(i);
Solve(H,L);
}
|
WQS二分+
可以与其它方法结合在一起,达到一个非常优秀的时间复杂度
关于WQS二分本身的内容这里就不多赘述了,可以去看其它文章理解一下,这里主要讲一下如何将其应用在决策单调性中
考虑一类问题:将一个序列强制分为k段,每一段\([l,r]\)有一个价值\(w(l,r)\),问总价值最小的分段
假设将序列分为k段的最优价值为\(f_k\),如果所有的\((k,f_k)\)组成一个凸函数,那么我们就可以使用WQS二分了。外层枚举斜率,内层就去掉了分段的限制,就可以使用二分队列/斜率优化/分治等措施了。
现在问题还是很多的,比如凸性的证明,WQS二分的边界问题,内部求最优值时更新的取等问题等。一个一个来
WQS多解情况
多解情况是指答案K与多个点在一条线段上,此时我们无法直接通过枚举斜率来做到只切到点K,所以我们需要在枚举的同时让得到的方案具有完全的偏序,来保证我们枚举斜率的时候,知道当前斜率对应的答案是哪一点的答案,是线段左端点的,还是右端点的,从而保证后面二分调整mid的时候不会弄混淆。很重要的一点是,我们需要的只是正确的斜率,不需要保证当前斜率做出来的最优点一定是K,因为\(f_k=mid*k+b\),其中斜率\(mid\)和截距\(b\)都是二分之后确定的值,在同一线段上的点做出的\(mid,b\)都是一样的。
那么为了做到严格偏序,我们需要对每一个属性都定义大小
这篇博客讲的很清晰,我可能讲的有点抽象,可以去再看看
满足四边形不等式的序列划分问题的答案凸性以及WQS二分的方案构造
这里我们尝试证明满足四边形不等式的序列划分问题都具有凸性
不妨先来看另一个问题:给定一张n个点的DAG,点\(i\)与点\(j\)当\(i<j\)时有权值\(w(i,j)\),问从1走到n的经过k条边的最短路
简单转化一下,这个问题的dp方程就是我们熟悉的:\(dp_{i,j}=min\{dp_{k,j-1}+w(k,i)\}\),\(dp_{i,j}\)表示走到i,经过j条边的最短路
设\(f_k\)表示经过k条边的最短路
下面我们尝试证明:当权值矩阵w满足四边形不等式的时候,\(f_k\)是一个下凸函数。换句话说,\(\forall k\in[2,n-2]\),\(f_{k+1}-f_k>f_k-f_{k-1}\)
引理:∀1 ≤ s < r
< t ≤ n − 1,
f(s) + f(t) ≥
f(r) + f(s + t −
r)
如果我们能够证明该引理的话,带入\(s=k-1,r=k,t=k+1\),则命题得证
下面尝试证明引理:
不妨记\(f_s\)对应的最优方案是\(p_1,p_2...p_{s+1}\),\(f_t\)对应的最优方案是\(q_1,q_2,..q_{t+1}\)
记\(v=r-s>0\),如果我们能够找到\(i \in [1,s]\),满足\(p_i\leq q_{i+v}<q_{i+v+1}\leq p_{i+1}(i+v+1\leq
s+v+1\leq t)\),就能够构造路径\(R_1:\)\(p_1,...p_i,q_{i+v+1},q_{i+v+2},..q_{t+1}\),以及路径\(R_2:\)\(q_1,...q_{i+v},p_{i+1},p_{i+2},...p_{s+1}\)(也就是把两段路径的后半段交换了一下,并且保证一定交换了一部分)
两段路径的长度分别是\(i-1+(t+1-i-v-1)+1=t-v=t-r+s\),以及\(i-1+v+(s+1-i-1)+1=s+v=r\),
那么由f的定义,\(R_1\)的路径长度\(len(R_1) \geq f_{t-r+s}\),\(R_2\)的路径长度\(len(R_2)\geq f_{r}\),
由四边形不等式\(w(p_i,q_{i+v+1})+w(q_{i+v},p_{i+1})\leq
w(q_{i+v}+q_{i+v+1})+w(p_i,p_{i+1})\)
故\(f_s+f_t\geq len(R_1)+len(R_2)\geq
f_{t-r+s}+f_r\)
第一个不等式是因为\(R_1,R_2\)与原本路径的区别只有中间衔接的一段
由上,我们只要证明存在这样的一个\(i\)即可。
 image-20230916142205317
image-20230916142205317
不妨记路径P将\((1,n]\)分成了s个部分,其中第i个部分是\((p_i,p_{i+1}]\)
我们记\(a_i\)表示\(q_{i+v}\)在哪一段,那么如果存在\(i\),\(a_i=a_i+1=k\),我们就找到答案为k了。
记\(b_i=a_i-i\),显然\(b_1\geq 0,b_{s+1}\leq -1\),后者是因为\(a_{s+1}-(s+1)\leq
s-(s+1)=-1\),此外显然\(b_i-b_{i-1}=0\)或\(-1\),故\(b_i-b_{i-1}\geq -1\)
由此序列b中一定存在一个-1,取最靠前的-1,记为\(b_{i+1}\).它前面一定是\(b_i=0\),故\(a_i=a_{i+1}\)
这样我们就找到了一个合法的\(i\),引理得证,故命题得证 Q.E.D
这段证明还是非常玄妙(玄幻)的。当然它对于我们的方案构造也有帮助
WQS二分中有时候会存在要求为k,但是\(k>l,k<r\)且\(l,r,k\)在一条线段上的情况,这时候我们一般通过限定边数尽可能多/少来保证取到线段的端点。但是想要构造方案的话就会不知所措了
我们记答案斜率为mid,这条包含答案k的线段的端点为\((l,f_l),(r,f_r)\),则\(\forall i\in[l,r],f_i=f_l+mid*(i-l)\)
我们可以先把\(l,r\)对应的最优方案找出来,长度分别为\(l,r\),那么按照上述证明中的构造方式我们得到长度为\(k,l+r-k\)的路径\(R_1,R_2\),记其路径长度分别为\(len(R_1)=a,len(R_2)=b\),有\(a\geq f_l+mid*(k-l),b\geq
f_l+mid*(l+r-k-l)\)
且有\(2f_l+mid*(k-l)+mid*(l+r-k-l)=2f_l+mid*(r-l)\leq
a+b\leq f_l+f_r=2f_l+mid*(r-l)\)
第二个不等号的原因见证明片段
发现\(a+b\)被边界夹住了,故\(a= f_l+mid*(k-l)\),由此a就是\(f_{k}\),我们就得到了长度为k的构造方案
以上内容参考 论文
《The d-Edge Shortest-Path Problem for a Monge
Grapll》,以及APIO2021《决策单调性与四边形不等式》
WQS外层二分时的边界
一般来说直接取\([-inf,inf]\)即可,或者稍微算一下卡住边界
不管是这样的
还是这样的
只要边界范围足够就不会有问题。但是有一类分段问题,图像长这样
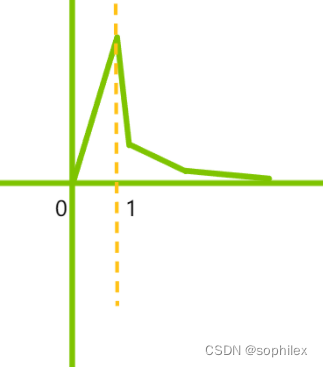
分段为0的时候,总价值为0,然后开始分段之后价值随分段减少。不考虑0的话,后面的一段也是满足凸函数的,那么这个对我们的边界会有影响吗?个人感觉没有,因为我们只要保证wqs二分之后在做最优决策的时候保证不让段数为0即可
比如这题就是这个情况CF321 E
(在分治部分此题作为练习出现,当然它也可以WQS二分,毕竟它满足四边形不等式,而我们已经证明了该类问题的凸性)
那么到这里,理论部分就差不多完善了,我们就可以看看应用了
不妨就看看这题CF321
E
按照套路,我们外层枚举斜率,内层就是每一段的贡献要减去一个\(mid\),问最优分段数及其对应的总贡献。dp式满足决策单调性,可以直接上单调队列,复杂度是\(O(nlogn^2)\),外层\(O(log)\),内层\(O(nlog)\),可以看到比普通的\(O(n^2log)\)分治要优化了不少
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
| #include <bits/stdc++.h>
#define pii pair<int,int>
#define il inline
#define ll long long
using namespace std;
const int N=4010;
const ll inf=1e18;
ll n,m;
ll mp[N][N];
ll cnt[N];
ll sum[N][N];
ll dp[N];
ll que[N];
ll ls[N],rs[N];
ll ANS;
ll cal(ll l,ll r)
{
return sum[r][r]-sum[l][r]-sum[r][l]+sum[l][l];
}
ll gt(ll k,ll x,ll val)
{
return dp[k]+cal(k,x)-val;
}
bool judge(ll x)
{
ll hd=1,tl=0;
que[++tl]=0;ls[0]=1,rs[0]=n;
for(int i=1;i<=n;++i)
{
cnt[i]=0,ls[i]=rs[i]=0;
while(hd<tl&&rs[que[hd]]<i) hd++;
dp[i]=gt(que[hd],i,x);
cnt[i]=cnt[que[hd]]+1;
while(hd<tl&>(i,ls[que[tl]],x)<gt(que[tl],ls[que[tl]],x)) tl--;
ll L=ls[que[tl]],R=n+1;
while(L<=R)
{
ll mid=(L+R)>>1;
if(gt(i,mid,x)<=gt(que[tl],mid,x)) R=mid-1;
else L=mid+1;
}
ll p_ans=R+1;
if(p_ans>n) continue;
rs[que[tl]]=p_ans-1;
que[++tl]=i;
ls[i]=p_ans,rs[i]=n;
}
ANS=dp[n];
return cnt[n]>=m;
}
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;++i)
{
for(int j=1;j<=n;++j)
{
cin>>mp[i][j];
if(i>j) mp[i][j]=0;
}
}
for(int i=1;i<=n;++i)
{
for(int j=1;j<=n;++j)
{
sum[i][j]=sum[i][j-1]+sum[i-1][j]+mp[i][j]-sum[i-1][j-1];
}
}
ll l=-1e18,r=0;
while(l<=r)
{
ll mid=(l+r)>>1;
if(judge(mid)) r=mid-1;
else l=mid+1;
}
judge(r+1);
cout<<ANS+m*(r+1)<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}
|
IOI2000 邮局
加强版
SDOI2016
征途
套路都差不多,套一个WQS的事,内层看情况用不同的优化手段
Akvizna
你面临 n 名参赛者的挑战,最终要将他们全部战胜。
每一轮中,都会淘汰一些选手;你会得到这一轮奖金池中 被淘汰者 除以
这一轮对手总数 比例的奖金。
例如某一轮有 10 个对手,淘汰了 3 个,那么你将获得奖金池中 3/10
的奖金。
假设每一轮的奖金池均为一元,Mirko 希望通过恰好
k 轮赢得比赛,那么他最多可能获得多少奖金呢?
你只需要输出答案保留 9 位小数即可。
这题略阴间,二分的时候不枚举小数的话过不了,肥肠卡精度,不过思维难度一般
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
| #include <bits/stdc++.h>
using namespace std;
#define ll long long
#define double long double
#define endl '\n'
const double eps=1e-12;
const ll inf=1e18;
const ll N = 1e5+10;
int n,m;
double dp[N];
double ANS;
double inv[N];
ll cnt[N];
ll que[N];
ll ls[N],rs[N];
double gt(ll k,ll x)
{
return dp[k]+(double)((x-k)*1.0*inv[n-k]);
}
bool judge(double x)
{
ll hd=1,tl=0;
que[++tl]=0;ls[0]=1,rs[0]=n;
for(int i=1;i<=n;++i)
{
cnt[i]=0,ls[i]=rs[i]=0;
while(hd<tl&&rs[que[hd]]<i) hd++;
cnt[i]=cnt[que[hd]]+1;
dp[i]=gt(que[hd],i)-x;
while(hd<tl&>(i,ls[que[tl]])>=gt(que[tl],ls[que[tl]])) tl--;
ll L=ls[que[tl]],R=n+1;
while(L<=R)
{
ll mid=(L+R)>>1;
if(gt(i,mid)>=gt(que[tl],mid)) R=mid-1;
else L=mid+1;
}
ll p_ans=R+1;
if(p_ans>n) continue;
rs[que[tl]]=p_ans-1;
que[++tl]=i;
ls[i]=p_ans,rs[i]=n;
}
ANS=dp[n];
return cnt[n]<=m;
}
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;++i) inv[i]=1.0/(i*1.0);
double l=-100,r=100;
while(l+eps<=r)
{
double mid=(l+r)/2.0;
if(judge(mid)) r=mid;
else l=mid;
}
judge(r);
cout<<fixed<<setprecision(9)<<ANS+m*1.0*(r)<<endl;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
solve();
return 0;
}
|
Tips:
做WQS二分一定要注意问题函数是一个上凸包还是下凸包
注意左右边界
有时候也是也是要二分小数的!
斜率优化
基本的斜率优化本人已经在另一篇博客中讲的很详细了,从入门到精通应该都有了。
然后更多的应用大概就是与WQS二分结合了吧
注意点好像也没啥,毕竟WQS二分之后内部就是一个纯纯的一维dp
SDOI2016
征途
Akvizna
值得一提的还有这道题JSOI2001 柠檬
之前在二分栈里提过它,但其实它也可以用斜率优化做,但是因为斜率实际上是递减的,所以内部维护凸包的时候是用一个栈(因为最优点在最后了,放入点也是在最后),这个还是比较少见的
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| #include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ld long double
#define IL inline
#define endl '\n'
const ll N=100010;
const ll mod=998244353;
const ll inf=1e18;
inline int read()
{
int X=0; bool flag=1; char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();}
while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();}
if(flag) return X;
return ~(X-1);
}
ll n,a;
ll dp[N];
vector<ll> col[N],st[N];
ll gt(ll x,ll c)
{
return dp[col[c][x]-1]+c*x*x-2*x*c;
}
double Slope(ll a,ll b,ll col)
{
if(a==b) return inf;
double x=gt(a,col)-gt(b,col);x=x*1.0;
double y=a-b;y*=1.0;
return x/y;
}
void solve()
{
cin>>n;
for(int i=1;i<=10000;++i) col[i].push_back(0);
for(int i=1;i<=n;++i)
{
cin>>a;
ll len=col[a].size();
col[a].push_back(i);
if(len==1) st[a].push_back(1);
else
{
while(st[a].size()>1&&Slope(st[a][st[a].size()-2],st[a][st[a].size()-1],a)<=2*a*len) st[a].pop_back();
ll id=st[a][st[a].size()-1];
dp[i]=dp[col[a][id]-1]+a*(1+len-id)*(1+len-id);
while(st[a].size()>1&&Slope(st[a][st[a].size()-2],st[a][st[a].size()-1],a)<=Slope(st[a][st[a].size()-1],len,a)) st[a].pop_back();
st[a].push_back(len);
}
dp[i]=max(dp[i],dp[i-1]+a);
}
cout<<dp[n]<<endl;
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}
|
一些特殊情况
可以看到,如果题目已经有了决策单调性,大部分情况下还是比较套路的,但是有些时候问题在全局上不满足决策单调性并不意味着局部也没有。
还是JSOI2001
柠檬这道题,它就是在同种颜色内部满足决策单调性(这么一看这真是道好题啊,哪哪都这么与众不同)
以及2016NAIP
H
大意:
有n个物品,每个物品有一个体积\(w_i\)和价值\(v_i\),现在要求对\(V∈[1,m]\),求出体积为\(V\)的 背包能够装下的最大价值
\(1≤n≤1000000;1≤m≤100000;1≤w_i≤300;1≤v_i≤10^9\)
其实就是对每一个\(V\),做一个多重背包
思路:
发现每一个物品的体积都比较小,所以可以按照体积分类。那么对于同一种体积的物品,我们肯定贪心选择价值最大的,所以可以排个序
考虑\(dp_{i,j}\)表示使用体积\(\leq
i\)的物品,总体积为j的最大价值。我们可以将所有需要更新的体积按照%i来重新编号。比如当前i是2,m是9,我们就可以将\(0,2,4,6,8\)化为一类各自重新编号为\(0,1,2,3,4\),\(1,3,5,7,9\)划为一类,编号同理
这样的好处就是我们对于每一个i,j的范围也只有\([0,i]\)这么大了,以及同一组体积内部的差恰好为i,那么物品就可以直接按照价值大小贪心塞了。
那么此时dp的意义就变了。如果当前是在更新%i=a的体积,则\(dp_{i,j}\)表示使用体积\(\leq i\)的物品,总体积为\(j*i+a\)的最大值
%i=a时,\(dp_{i,j}=max_{k\leq
j}\{dp_{i-1,k}+w(k,j)\}\),其中\(w(k,j)\)表示体积=i的物品中最大的\(j-k\)个物品的价值和,记为前缀和\(vt_{i,j-k}\)
简单证一下四边形不等式:
考虑\(i,i+1,j,j+1,i+1<j\)
\(w(i,j)+w(i+1,j+1)=2vt_{j-i}\)
\(w(i+1,j)+w(i,j+1)=vt_{j-i-1}+vt_{j-i+1}=2vt_{j-i}+a_{j-i+1}-a_{j-i-1}\leq
w(i,j)+w(i+1,j+1)\)
得证
那么直接分治即可
code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| #include <bits/stdc++.h>
using namespace std;
#define ll long long
#define double long double
#define endl '\n'
const double eps=1e-11;
const ll inf=1e18;
const ll N = 1e6+10;
ll n,m;
vector<ll> vt[310];
ll dp[N],pp[N];
ll gt(ll id,ll x,ll mod,ll res)
{
return pp[id*mod+res]+vt[mod][x-id-1];
}
bool cmp(ll a,ll b)
{
return a>b;
}
void Solve(ll l,ll r,ll pl,ll pr,ll mod,ll res)
{
if(l>r) return;
ll mid=(l+r)>>1;
ll pos=mid;
dp[mid*mod+res]=pp[mid*mod+res];
for(int i=min(mid-1,pr);i>=pl;--i)
{
if(mid-i>(int)vt[mod].size()) break;
if(gt(i,mid,mod,res)>dp[mid*mod+res]) dp[mid*mod+res]=gt(pos=i,mid,mod,res);
}
Solve(l,mid-1,pl,pos,mod,res);
Solve(mid+1,r,pos,pr,mod,res);
}
void solve()
{
cin>>n>>m;
for(int i=1;i<=n;++i)
{
ll a,b;
cin>>a>>b;
vt[a].push_back(b);
}
for(int i=1;i<=300;++i)
{
sort(vt[i].begin(),vt[i].end(),cmp);
for(int j=1;j<(int)vt[i].size();++j) vt[i][j]+=vt[i][j-1];
}
for(int i=1;i<=300;++i)
{
if(!vt[i].size()) continue;
for(int j=0;j<i;++j)
{
Solve(0,(m-j)/i,0,(m-j)/i,i,j);
}
for(int j=1;j<=m;++j) dp[j]=max(dp[j],dp[j-1]);
for(int j=1;j<=m;++j) pp[j]=max(dp[j],dp[j-1]);
}
for(int i=1;i<=m;++i) cout<<pp[i]<<" ";
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
solve();
return 0;
}
|
本来想用SMAWK写的,但是一直MLE,不懂,求懂的佬教教
当然这题的决策单调性也是分组才有的,很抽象,感觉本人是不可能看出来的(哭
总结:
大工程,希望对自己&大家有用:heartpulse:
参考文章
OIWIKI
Bein, W W, Larmore, L
L, and Park, J K. The d-edge shortest-path problem for a Monge
graph. United States: N. p., 1992. Web.
Bein, W W, Brucker, P,
and Park, J K. Applications of an algebraic Monge property.
United States: N. p., 1993. Web.
Divide
and Conquer DP
决策单调性
- MCAdam
关于决策单调性与图像的结合
彭思进 《决策单调性与四边形不等式》







