LightGCN:简化和增强图卷积网络的推荐

Abstract

图卷积网络 (GCN) 已成为协同过滤的最新技术。然而，它推荐有效性的原因并没有得到很好的理解。该工作还发现 GCN 中最常见的两种设计——特征变换和非线性激活——对协同过滤的性能贡献不大，并且还增加了训练的难度，降低了推荐性能。 在这项工作中，作者提出了一种新的模型LightGCN，只包含GCN中最基本的组件——邻域聚合。具体来说，LightGCN 通过在用户-项目交互图上线性传播来学习用户和项目嵌入，并使用所有层学习到的嵌入的加权和作为最终嵌入。这种简单、线性和整洁的模型更容易实现和训练，与同一个组之前提出的NGCF相比，有明显的改进（平均约 16.0% 的相对改进）。最后对LightGCN的合理性进行了分析。 本文的主要贡献： * 通过实验说明GCN中的非线性激活以及特征变换对协同过滤没有积极影响 * 提出了LightGCN，结构更加简洁，并且性能更好 * 对LightGCN的合理性进行分析 ## NGCF 先简单介绍一下NGCF。 NGCF主张在协同过滤中加入对user-item对信息的编码，而不仅仅是只考虑user，item的emmbedding，从而能够获得更多信息，进而进行推荐。实际场景中user-item对的信息很多，所以它借鉴了GCN中的领域聚合的思想，仿照GCN的结构，每一层聚合周围邻居的信息，从而在多层之后实现对多跳邻居的信息的收集。 具体来说，每一层的信息传播公式为 \[ m_{u\leftarrow i}^{(l)}=\frac{1}{\sqrt{|N_u||N_i|}}(W_1^{(l)}e_i^{(l-1)}+W_2^{(l)}(e_i^{(l-1)}⊙e_u^{(l-1)})) \] \[ m_{u\leftarrow u}^{(l)}=W_1^{(l)}e_u^{(l-1)} \]

这是对user而言的，item的传播公式同理 其中\(m_{u\leftarrow i}\)表示\(item_i\)与\(user_u\)之间的协作信息，\(\frac{1}{\sqrt{|N_u||N_i|}}\)借鉴了GCN的思路，不过作者在文中把它理解为信息的衰减系数，也就是当前信息应该随着层的传播而比重变小。考虑到自己到自己的信息不用衰减，所以第二个式子没有乘上对称归一化的系数。\(W_1,W_2\)是可训练系数，\(e_i,e_u\)就是item和user的当前特征embedding，最后加了一个\(e_i⊙e_u\),也就是两者的哈达玛积，用来编码两者的信息交互（有点像attention？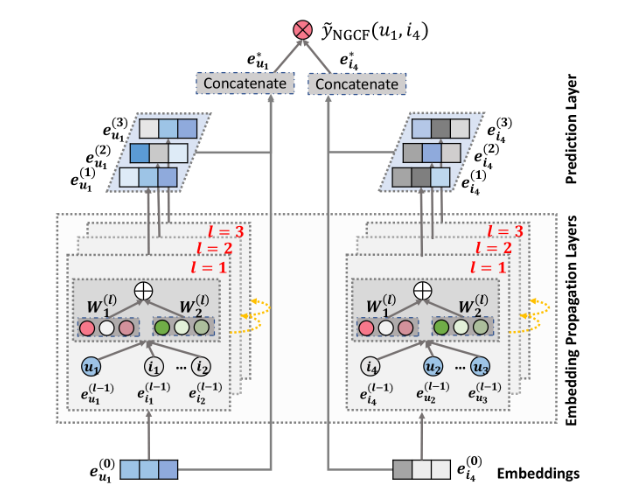） 最后得到每一层的新的特征表示： \[ e_u^{(l)} = LeakyReLU(m_{u\leftarrow u}^{(l)}+\sum_{i\in N_u}m_{u\leftarrow i}^{(l)}) \] 这是NGCF的基本结构。首先在embedding层获得每一个user，item的embedding，这里展示了\(e_{u_1}^{(0)}\)以及\(e_{i_4}^{(0)}\)的embedding。然后逐层传播并更新每一层的embedding，在最后一层将每一层的embedding进行拼接，然后拿去做预测。 这里拼接应该也是为了进行特征增强，不过后面LightGCN也还是改掉了。

LightGCN

可以看到NGCF其实大量借鉴了GCN的结构，但是其中也有一些操作是毫无理由就搬上来了。所以作者对其进行了大量的消融分析，包括对非线性激活和特征变化结构的质疑。 作者建立了四个模型进行比较，分别是 * NGCF,也就是原模型 * NGCF-n 去掉了特征变换，也就是上一节中的\(W_1,W_2\)参数矩阵的NGCF * NGCF-f 去掉了非线性激活的NGCF * NGCF-fn 去掉了特征变换以及非线性激活的NGCF 然后在\(Gowalla\)和\(Amazon-Book\)数据集上进行测试，得到结果如下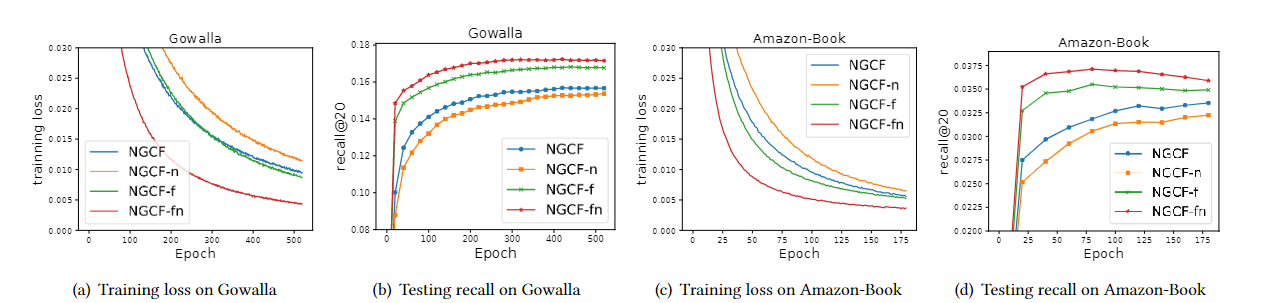： 可以看出NGCF-fn的性能是远好于NGCF的，作者将这一点归因于特征变换以及非线性激活操作加大了训练的难度，从而提出对其进行简化，得到如下的传播公式 \[ e_{u}^{(k+1)}=\sum_{i\in N_u}\frac{1}{\sqrt{|N_u||N_i|}}e_i^{(k+1)}\\ e_{i}^{(k+1)}=\sum_{u\in N_i}\frac{1}{\sqrt{|N_u||N_i|}}e_u^{(k+1)} \] 在最后一层进行每一层特征的加权求和得到最终特征 \[ e_u=\sum_{k=0}^{K}\alpha_ke_u^{(k)}\\ e_i=\sum_{k=0}^{K}\alpha_ke_i^{(k)} \] 最终得到user-item项目的最终得分为 \[ \hat{y}_{ui}=e_u^{T}e_i \] 上面的式子不方便实现，我们将其转换为矩阵形式 假设user有\(N\)个，item有\(M\)个，每一个user/item的特征长度为\(T\),那么定义邻接矩阵\(A\in R^{(N+M)\times(N+M)}\)表示user-item的邻接矩阵，矩阵\(E\in R^{(N+M)\times T}\)表示每一个user/item的embedding，显然\(E^{0}\)就表示了大家的初始embedding。再定义矩阵\(D\in R^{(N+M)\times(N+M)}\)表示度数矩阵。 从而得到传播公式为 \[ E^{k+1} = (D^{-\frac{1}{2}}AD^{-\frac{1}{2}})E^{k} \] 最终每一个user/item的embedding为 \[ E = \alpha_0E^{0}+\alpha_1E^{1}+....+\alpha_KE^{K}=\alpha_0E^{0}+\alpha_1\tilde{A}E^{0}+....+\alpha_K\tilde{A}^{K}E^{0}=\sum_{i=0}^{K}\alpha_i\tilde{A}^iE^0 \] 其中\(\tilde{A}=D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\)

---

与NGCF的式子进行对比，可以发现LightGCN总共去掉了如下几个构造： * 特征变换，非线性激活 * 自连接 * user-item的哈达玛积 对于哈达玛积的移除作者没有详细介绍，只是在后面实验时提了一嘴LightGCN效果比NGCF-fn效果更好，所以可能也没啥用，就移掉了。 除此之外，在实现细节上，LightGCN相比GCN还有如下变化 * 在最后一层将每一层特征的concat操作变成了加权求和 * 去掉了每一层的dropout操作 ## 模型分析 分析一下每一个操作的合理性 ### 加权求和与去除自连接 作者去除自连接的原因与最后一步的加权求和有关系。注意到最后的特征表示为 \[ E =\sum_{i=0}^{K}\alpha_i\tilde{A}^iE^0 \] 这与之前的一些工作具有相同的形式，所以作者指出该模型同样可以享用它们的优点 #### SGCN 这是之前的一篇简化GCN的工作，它同样是去除了非线性激活函数，并且将每一层的权重矩阵简化成了一个，其传播公式为 \[ E^{(k+1)}=(D+I)^{-\frac{1}{2}}(A+I)(D+I)^{-\frac{1}{2}}E^{k} \] 它包含了自连接操作，我们将其在式子中提取出来了，然后进行化简，得到 \[ E^{(k)}=(\tilde{A}+(D+I)^{-1})E^{k-1}=(\tilde{A}+(D+I)^{-1})^KE^{0}=(\tilde{A}+\tilde{D})^KE^0 \] 其中 \[ \tilde{A}=D^{-\frac{1}{2}}AD^{-\frac{1}{2}},\tilde{D}=(D+I)^{-1} \] 对前面的系数二项展开，得到 \[ E^{(k)}=\binom{K}{0}\tilde{D}^KE^{0}+\binom{K}{1}\tilde{D}^{K-1}AE^{0}+...+\binom{K}{K}A^KE^{0}=\sum_{i=0}^{K}\binom{K}{i}\tilde{D}^{K-i}\tilde{A}^iE^0 \] 没错，与LightGCN的式子相比还多了一个对角矩阵，形式上是不一样的。原文是用另一个方法推导的，省略了\((D+I)^{-\frac{1}{2}}\),理由是它只缩放了embedding，但是个人认为每一维的缩放系数不同，不能直接这样忽略。这里存疑。 总之作者在这里得到结论是两个模型在结构上相同，所以没有添加自环也没有关系，实际效果上已经添加了。 #### APPNP 这个工作宣称可以在没有过度平滑的风险的情况下传播远程，其传播公式为 \[ E^{K}=\beta E^0+(1-\beta)\tilde{A}E^{K-1} \] 显然这是一个可以求通项的式子，化简得到 \[ E^{K}=\beta E^0+(1-\beta)\tilde{A}E^{K-1}\\ =\beta E^0+\beta(1-\beta)\tilde{A}E^{0}+(1-\beta)^2\tilde{A}^2E^{K-2}\\ =\beta E^0+\beta(1-\beta)\tilde{A}E^{0}+(1-\beta)^2\tilde{A}^2E^{0}+...+(1-\beta)^K\tilde{A}^KE^0 \]

注意到该式子与LightGCN的传播公式也就只有系数差别，所以LightGCN在减少过拟合方面有较好的效果，后面的实验也佐证了这一点

去除哈达玛积

作者引入它是为了强调user-item的交互，有点类似attention，但是个人感觉模型已经是在gcn的基础上做改进了，而gcn的一个最大特点就是逐层聚合邻域信息，这一点本身就已经在实现信息的交互了，所以可能这也是在LightGCN中将其移除的原因吧

去除dropout

注意到LightGCN整个模型其实已经只有初始化embedding的一些矩阵参数了，每一层传播的时候是没有参数的了，所以也没有做dropout的必要了，\(L_2\)正则化就足够保证避免过拟合了

嵌入的平滑性

我们考虑两个共享同一个item的节点的信息传递

\[ e_u^{(2)}=\sum_{i\in N_u}\frac{1}{\sqrt{|N_u||N_i|}}e_i^{(1)}=\sum_{i\in N_u}\frac{1}{|N_i|}\sum_{v\in N_i}\frac{1}{\sqrt{|N_u||N_v|}}e_v^{(0)} \] 注意到\(user_v\)与\(user_u\)之间的信息传递的系数为 \[ c_{v\rightarrow u}\frac{1}{\sqrt{|N_u||N_v|}}\sum_{i\in N_u\cap N_v}\frac{1}{|N_i|} \] 这一系数符合很多直观的想法，二阶邻居 v 对 u 的影响由 1) 共同交互项目的数量、越大； 2) 共同交互项目的流行程度越低（即更能指示用户个性化偏好）越大； 3) v 的活动，越大越活跃。 这种可解释性很好地满足了 CF 在测量用户相似度 中的假设，并证明了 LightGCN 的合理性。

留的坑

作者在文末指出对\(\alpha_i\)的个性化调节，即稀疏用户可能需要更多来自高阶邻居的信号，而活动用户只需要更少

总结

总体来说，LightGCN在NGCF的基础上，指出特征变换与非线性激活在推荐模型上的冗余性，充分简化了其模型结构，并且提高了性能。但是这是建立在推荐的场景下，原始的GCN是用于节点分类的，此时每一个节点包含更多信息，而不是只有id信息，所以还是需要非线性激活与特征变换的。